Úloha: Počet ostrovov

Na vstup dostanete 2d mapu 1-čiek (pevnina) a 0 (voda), spočítajte koľko ostrovov sa na tejto mape nachádza. Ostrov je tvorený všetkými jednotkami, do ktorých sa dá dostať postupnosťou horizontálnych a vertikálnych posunov.

Príklad 1

Vstup

11110
11010
11000
00000

Výstup

1

Príklad 2

Vstup

11000
11000
00100
00011

Výstup

3

Poznámky:

• bludisko načítavajte zo súboru a výstup vypíšte do konzole
• môžete predpokladať, že na vstup dostanete vždy rozumné bludisko (tzn. nie je treba ošetrovať nesprávny vstup)
• bludisko na vstupe môže mať rôzne rozmery
• hint: použite vhodné prehľadávanie, môžete používať dátové štruktúry naimplementované priamo v C#, e.g. Queue<T>.

Vaše riešenie aj s testovacím kódom mi pošlite mailom (posielajte len čisté zdrojáky).

Úloha: Bludisko

Nájdite najkratšiu cestu z bludiska:

Príklad

Vstup

+-+-+-+-+-+-+-+-+-+-+
    |       |       |
+-+ + +-+-+ + +-+-+-+
|   | |       |     |
+ +-+-+ +-+ + + +-+ +
| | |   |   |   | | |
+ + + +-+ +-+-+-+ + +
|   | |   |   | |   |
+ +-+ + +-+-+ + +-+-+
| |   |   |   |   | |
+ + +-+-+ + +-+-+ + +
|   |     | |   |   |
+-+-+ +-+-+ +-+ +-+ +
|     |     |     | |
+ +-+-+ +-+-+ +-+ + +
|   | |     |   |   |
+-+ + +-+-+ +-+ +-+-+
|   |       |       |
+ +-+ + +-+-+ +-+-+ +
|     |       |      
+-+-+-+-+-+-+-+-+-+-+

Výstup

+-+-+-+-+-+-+-+-+-+-+
####|       |       |
+-+#+ +-+-+ + +-+-+-+
|###| |#####  |     |
+#+-+-+#+-+#+ + +-+ +
|#| |###|###|   | | |
+#+ +#+-+#+-+-+-+ + +
|#  |#|###|   | |   |
+#+-+#+#+-+-+ + +-+-+
|#|###|###|   |   | |
+#+#+-+-+#+ +-+-+ + +
|###|#####| |   |   |
+-+-+#+-+-+ +-+ +-+ +
|#####|     |     | |
+#+-+-+ +-+-+ +-+ + +
|###| |     |   |   |
+-+#+ +-+-+ +-+ +-+-+
|###|###    |#######|
+#+-+#+#+-+-+#+-+-+#+
|#####|#######|    ##
+-+-+-+-+-+-+-+-+-+-+

Poznámky:

• bludisko načítavajte zo súboru a výstup vypíšte do konzole
• môžete predpokladať, že na vstup dostanete vždy rozumné bludisko (tzn. nie je treba ošetrovať nesprávny vstup)
• bludisko na vstupe môže mať rôzne rozmery
• viete sa hýbať len v štyroch smeroch: hore, dole, doprava, doľava
• nájdená cesta musí byť najkratšia
• do bludiska vstupujete vždy z ľavého horného rohu a vystupujete z práveho dolného rohu
• vaše riešenie si otestujte aspoň na niekoľkých ďalších vstupoch, ktoré si vygenerujte tu: Maze Generator
• hint: použite vhodné prehľadávanie, môžete používať dátové štruktúry naimplementovanú priamo v C#, e.g. Queue<T>.
• chcem vidieť pekne štrukturovaný kód, tzn.:
  • rozumné využitie tried
  • žiadna metóda by nemala mať viac než 10 riadkov

Vaše riešenie aj s testovacím kódom mi pošlite mailom (posielajte len čisté zdrojáky).

Ďalšie cvičenie odpadáva, opravný termín bude až o 2 týždne.

Úloha č. 1: Fibonacci

Aké sú problémy implementácie výpočtu n-tého Fibonacciho čísla nižšie?

Ako by ste túto implementáciu vylepšili?

public static int fibonacci(int n) {
  if (n == 0) return 0;
  if (n == 1) return 1;
  return fibonacci(n - 1) + fibonacci(n - 2);
}

Úloha č. 2: Subset sum

Napíšte program, ktorý zistí, či je možne z množiny prirodzených čísel M vybrať podmnožinu so súčtom s a túto podmnožinu aj vypíše.

Príklad: Pre s = 7 a M = {1, 4, 9, 3} program vráti True a {3, 4}.

Začnite tým, že vypíšete True resp. False v prípade existencie takej podmnožiny resp. neexistencie.

Úloha č. 3: : Štvorcová podmatica

Napíšte program, ktorý pre zadanú 0/1 maticu vypíše velkosť jej najväčšej štvorcovej podmatice obsahujúcej len jednotky. Napr. pre maticu nižšie vypíše 3.

1 1 1 1 0
0 1 1 1 1
0 1 1 1 1
1 0 1 1 1
0 1 1 1 0

Domáca úloha č. 1 a 2: Maximální palindrom a Loupežníci

Zadania nájdete v CodEx-e.

Poznámka:

• na vyriešenie oboch úloh musíte použiť dynamické programovanie
• ak by vám to zas hádzalo time limit exceeded, tak to riešiť nebudem

Termín odovzdania: 7. 5. 2017(23:59)

Spôsob odovzdania: CodEx (odovzdávajte hlavný zdroják obsahujúci metódu main)

Počet bodov: 20 a 30

Úloha č. 1: Aplikácia stopky

Pomocou WinForms naprogramujte aplikáciu stopky podobnú tej na obrázku nižšie:

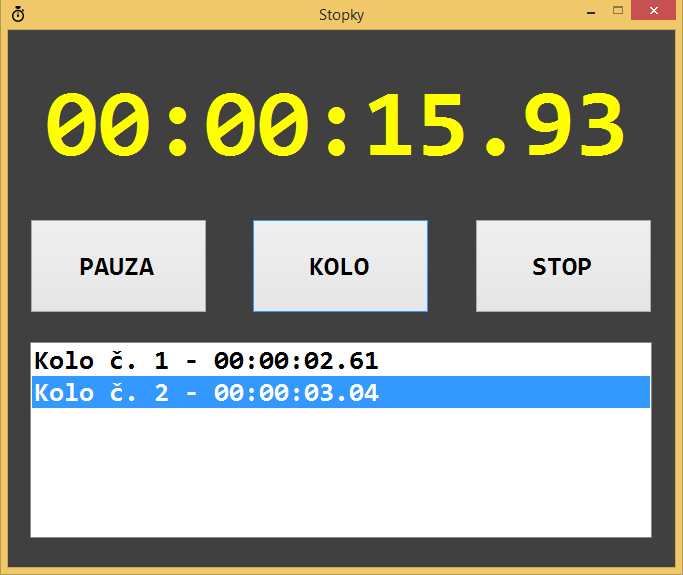
Funkcionalita:

• tlačítka
  • štart/pauza - naštartuje stopky alebo preruší stopky
  • reset - zresetuje čas na stopkách
  • kolo - uloží aktuálny čas na stopkách

Poďakovanie: Za nápad a zdrojové kódy k aplikácii ďakujem Jiřímu Novotnému.

Úloha č. 1: CharReader

Vytvorte dve implementácie ICharReader-u, jedna bude po jednom načítavať znaky z konzole a druhá zo súboru. Použite šablonu nižšie.

interface ICharReader {
  char nextChar();
}

class ConsoleCharReader : ICharReader {
  public char nextChar() {
      throw new NotImplementedException();
  }
}

class FileCharReader : ICharReader {
  public char nextChar() {
      throw new NotImplementedException();
  }
}

Úloha č. 2: WordReader

Pomocou naimplementovaných ICharReader-ov z úlohy 1 vytvorte WordReader, ktorý bude schopný načítavať stream po slovách. Použite šablonu nižšie. Čo presne slovo je nechám na vás, úplne postačí sekať stream po medzerách.

Otestuje svoju implementáciu s ConsoleCharReader-om aj FileCharReader-om.

class WordReader {
  ICharReader reader;
  public WordReader(ICharReader reader) {
    this.reader = reader;
  }

  public String nextWord() {
    // doimplementujte
  }
}

Domáca úloha: Aproximácia čísla π

Názvom Monte Carlo sa označuje rodina algoritmov, ktorá pri riešení problémov používa náhodu. Tento prístup je možné jednoducho ilustrovať na aproximácii čísla π.

Predstavte si kruh vo štvorci:

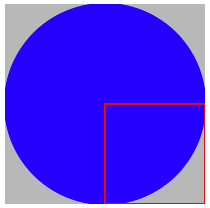
1. Obsah modrého kruhu spočítate ako $πr^2$
2. Obsah sivého štvorca zas ako $4r^2$
3. Pomer obsahu kruhu voči štvorcu je teda $p=\frac{πr^2}{4r^2}=\frac{π}{4}$
4. Takže hodnotu π dostaneme ako $π=4p$
5. Stačí uvažovať červený výsek, pomer $p$ je rovnaký a uľahčí nám to jeho výpočet.

Samotný algoritmus bude uvažovať kruh s polomerom 1, tzn. že veľkosť hrany štvorca v červenom výseku je tiež 1. Predstavte si, že stred kruhu je v súradnici 0,0. Algoritmus Monte Carlo začne náhodne generovať body v tomto štvorci a skontroluje či sa tento bod nachádza aj vo výseku modrej kružnice. Pomer bodov v kruhu voči všetkým vygenerovaným bodom nám dáva aproximáciu hľadaného $p$. Čím viac bodov vygenerujete, tým lepšiu aproximáciu $p$, tzn. aj $π$ dostanete. Počet vygenerovaných bodov musí byť parametrizovateľný, vyskúšajte ako počet bodov ovplyvňuje presnosť odhadu.

Podľa popisu vyššie naimplementujte tento algoritmus v C# a zdroják mi pošlite mailom. Zdroják by mal obsahovať aj testovací kód a implementácia by mala byť v nejakej triede, nechcem vidieť statické metódy.

Termín odovzdania: 9. 4. 2017 (23:59)

Spôsob odovzdania: zdrojový kód mailom

Počet bodov: 20